(
Ολα τα παρακατω ειναι
AΠΟ ΕΔΩ!, οποτε, αναλογως και τα αναλογουντα "ευσημα"!

Ειναι αρκετα, αλλα
πολυ διαφωτιστικα!

)
Εισαγωγή
Το άρθρο αυτό σκοπεύει στο να διασαφηνίσει ένα σημαντικό θέμα, αυτό της ισχύος και της ροπής όσον αφορά τα αυτοκίνητα και τις μοτοσικλέτες. Είναι κάτι που το συναντάμε παντού. Στις δοκιμές των περιοδικών και σε διαφημίσεις ή ανακοινώσεις των κατασκευαστών για κάθε όχημα δίνεται η τιμή της μέγιστης ισχύος, της μέγιστης ροπής και φυσικά οι στροφές λειτουργίας όπου οι τιμές αυτές αποδίδονται.
Αν και θεωρούμε την γνώση του δεδομένη, στην πραγματικότητα μάλλον αγνοούμε πλήρως την ουσία του και το τι εκφράζει. Εδώ θα εξετάσουμε το θέμα από την αρχή και σφαιρικά ενώ στο τέλος του άρθρου παρατίθονται κάποια παραδείγματα με πραγματικά δεδομένα για καλύτερη κατανόηση του θέματος.
Υπάρχουν αρκετά στερεότυπα επάνω στο το τι ακριβώς αντιπροσωπεύει η ισχύς και η ροπή ενός αυτοκινήτου ή μοτοσικλέτας. Μερικά από αυτά λένε πως "η ισχύς μας δείχνει πόσο γρήγορο είναι ένα αυτοκίνητο και η ροπή πόσο δυνατό", "για δύναμη σε χαμηλές ταχύτητες χρειαζόμαστε μεγάλη ροπή σε χαμηλές στροφές", "ένα ντίζελ αυτοκίνητο είναι πιο δυνατό από ένα 'πολύστροφο' βενζινοκίνητο μεγαλύτερης ισχύος" κ.α.
Τα παραπάνω φυσικά είναι είτε υπέρ-απλουστεύσεις είτε εντελώς λανθασμένες απόψεις που όμως για κάποιον που έχει πλήρη άγνοια του αντικειμένου μπορούν να περιγράψουν αποσπασματικά την αίσθηση που δίνει κάποιο αυτοκίνητο, για τον λόγο αυτό άλλωστε έχουν επικρατήσει και καθιερωθεί τόσα χρόνια.
Για τον λόγο αυτό ξεκινάμε από τα βασικά:
Ενέργεια, ισχύς
Το ζητούμενο από ένα αυτοκίνητο (ή μοτοσικλέτα) είναι να μπορεί να μεταφέρει το φορτίο του (επιβάτες κλπ) και να μπορεί να επιταχύνει ή να διατηρεί την ταχύτητά του σε ανηφόρες ή όταν επικρατούν δυσμενείς εξωτερικές συνθήκες. Για το λόγο αυτό υπάρχει προφανώς ο κινητήρας ο οποίος παράγει ενέργεια η οποία θα καταλήξει εν τέλει στα λάστιχα και θα ωθήσει το όχημα. Στους εμβολοφόρους ΜΕΚ των αυτοκινήτων η παραγωγή ενέργειας εξαρτάται από πολλές παραμέτρους, αν θεωρήσουμε πως εδώ εξετάζουμε την λειτουργία των κινητήρων υπό πλήρες φορτίο και απλοποιώντας εξωγενείς παράγοντες (ποιότητα καυσίμου, θερμοκρασία περιβάλλοντος κλπ) τότε μπορούμε με καλή προσέγγιση να θεωρήσουμε πως ο κινητήρας παράγει ενέργεια σε συνάρτηση με τις στροφές περιστροφής του.
Δηλαδή για το μέγεθος της ισχύς (παραγωγή ενέργειας στη μονάδα του χρόνου) θεωρούμε πως ένας κινητήρας σε συγκεκριμένες στροφές παράγει πάντα την ίδια ισχύ (πχ στις 3500rpm αποδίδει 100ps).
Αν ρίξουμε μια ματιά σε ένα οποιοδήποτε διάγραμμα ισχύος όπως το παρακάτω θα δούμε πως κάθε κινητήρας έχει συγκεκριμένο φάσμα λειτουργίας και αν θέλουμε να έχουμε την μέγιστη δύναμη στους κινητήριους τροχούς (για να επιταχύνουμε ή για να υπερκεράσουμε κάποιο εμπόδιο, πχ ανηφόρα) τότε θα πρέπει να βρούμε ένα τρόπο ώστε να λειτουργούμε τον κινητήρα στις στροφές όπου αποδίδει το μέγιστο της ισχύος του.
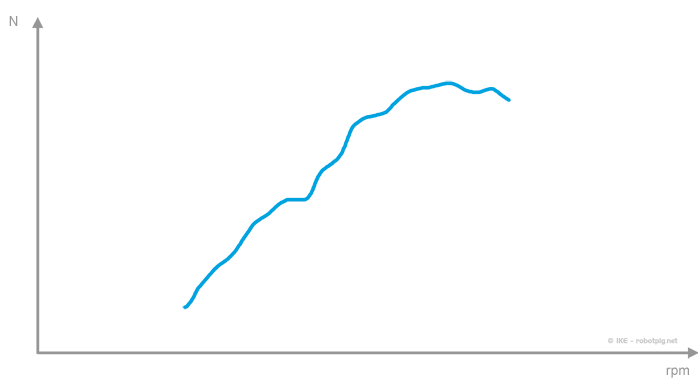
Ο κινητήρας συνδέεται με τους τροχούς με τη βοήθεια του συστήματος μετάδοσης, οπότε η ταχύτητα περιστροφής του εξαρτάται άμεσα από την ταχύτητα που κινείται το όχημα. Το σύστημα μετάδοσης (κιβώτιο ταχυτήτων, διαφορικό και τροχοί) είναι αυτό που με τον κατάλληλο 'συγχρονισμό' της ταχύτητας περιστροφής του κινητήρα και της ταχύτητας κίνησης του αυτοκινήτου θα μας βοηθήσει να διατηρούμε τις στροφές λειτουργίας του κινητήρα στο σημείο όπου παράγει την επιθυμητή ισχύ για οποιαδήποτε ταχύτητα κίνησης.
Μέχρι τώρα αναφερθήκαμε στην ισχύ αλλά όχι στην ροπή, όπως θα δούμε και στην επόμενη παράγραφο η ροπή είναι ένα μέγεθος που μεταβάλλεται συνέχεια στα διάφορα στάδια μεταξύ κινητήρα και τροχού ενώ η ισχύς είναι το μέγεθος αυτό που παραμένει αναλλοίωτο (εξαιρουμένων φυσικά των απωλειών).
Ροή ισχύος
Ποια είναι λοιπόν η σχέση μεταξύ ροπής και ισχύος? Σε ένα μη περιστρεφόμενο σύστημα, αν για παράδειγμα έχουμε μια μάζα που μετακινείται ευθύγραμμα, η ισχύς με βάση τη Νευτώνεια μηχανική μας δίνεται από τον ρυθμό μεταβολής της ενέργειας. Αν θέλουμε να συμπεριλάβουμε το μέγεθος της ταχύτητας με απλές πράξεις προκύπτει πως η ισχύς δίνεται από το γινόμενο ταχύτητας επί την δύναμη.
Δηλαδή για να μετακινήσουμε ένα βαρύ κιβώτιο με μικρή ταχύτητα θα καταναλώσουμε ίδια ισχύ με το να μετακινήσουμε ένα ελαφρύ κιβώτιο με μεγάλη ταχύτητα. Στην περίπτωσή μας όπου το σύστημα είναι περιστρεφόμενο η ισχύς ισοδυναμεί με το γινόμενο της γωνιακής ταχύτητας (στροφές ανά λεπτό) επί την ροπή στρέψης, οπότε για δεδομένη ισχύ μπορούμε είτε να έχουμε μεγάλη ροπή και χαμηλή ταχύτητα περιστροφής είτε μικρή ροπή και υψηλή ταχύτητα περιστροφής.
Για την καλύτερη κατανόηση των μεγεθών της ισχύος, της ροπής και της ταχύτητας περιστροφής χρησιμοποιούμε τα παρακάτω διαγράμματα με το τετράγωνο ισχύος (περισσότερα στο κουτάκι δεξιά).
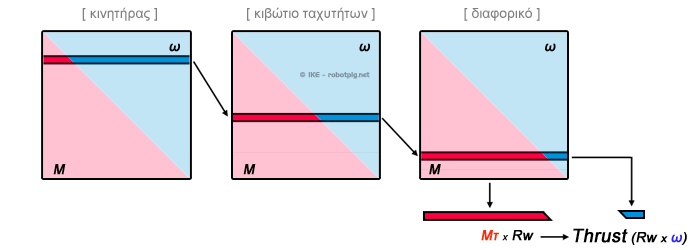
(Μ=ροπή, ω=γωνιακή ταχύτητα, Thrust=ώση, Rw=ακτίνα τροχού)
Στο παραπάνω σχήμα βλέπουμε πως το -σταθερό- ποσό ισχύος που παράγει ο κινητήρας (σε συγκεκριμένες στροφές) αντιπροσωπεύεται από το πλάτος του κάθε τετραγώνου. Σε κάθε στάδιο του συστήματος μετάδοσης μπορούμε να επιλέξουμε όποια 'στάθμη' του τετραγώνου μας βολεύει ώστε να έχουμε τον επιθυμητό συνδυασμό rpm και ροπής. Ο συνδυασμός αυτός στο τελικό στάδιο θα αντιστοιχήσει την ταχύτητα κίνησης του οχήματος με την ανάλογη γωνιακή ταχύτητα και η τελική ροπή πολλαπλασιαζόμενη με την ακτίνα του τροχού θα μας δώσει την δύναμη που ασκείται στο δρόμο (ώση).
Μια παρατήρηση εδώ, το σύστημα μετάδοσης είναι πολύ σημαντικό, ίσως εξίσου σημαντικό με τον κινητήρα, όπως βλέπουμε και στο παρακάτω σχήμα μπορούμε να φτάσουμε στο ίδιο αποτέλεσμα ώσης στον τροχό (σε συγκεκριμένη ταχύτητα) από δύο διαφορετικούς κινητήρες (Κ1 και Κ2 στο σχήμα) με εντελώς διαφορετικά χαρακτηριστικά λειτουργίας αν χρησιμοποιήσουμε διαφορετικούς λόγους μετάδοσης στο κιβώτιο ταχυτήτων:
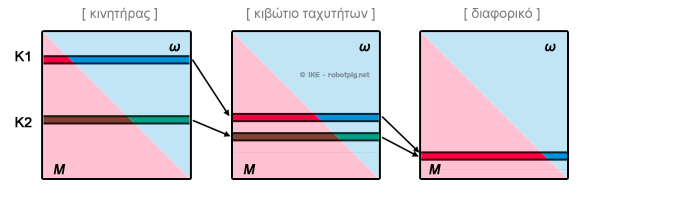
Αν είχαμε μόνο μια σταθερή σχέση μετάδοσης (συγκεκριμένες στροφές ανά λεπτό λειτουργίας του κινητήρα να αντιστοιχούν σε συγκεκριμένη ταχύτητα κίνησης) τότε θα μπορούσαμε να εκμεταλλευτούμε το φάσμα της λειτουργίας του κινητήρα στο μέγιστο της απόδοσής του μόνο σε πολύ συγκεκριμένες ταχύτητες κίνησης.
Για το λόγο αυτό λοιπόν υπάρχει το κιβώτιο ταχυτήτων. Χρησιμοποιώντας το μπορούμε να ρυθμίζουμε τον συσχετισμό ταχύτητας κίνησης οχήματος και ταχύτητας περιστροφής κινητήρα ώστε να χρησιμοποιήσουμε το ωφέλιμο πεδίο λειτουργίας του σε ένα ευρύτερο φάσμα ταχυτήτων κίνησης του οχήματος:
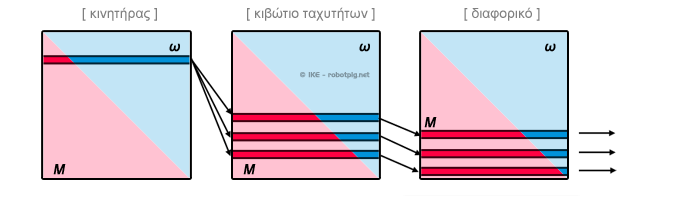
Βλέπουμε εδώ πως με 3 ταχύτητες μπορούμε να λειτουργούμε τον κινητήρα στη μέγιστη ισχύ για 3 συγκεκριμένες ταχύτητες κίνησης, στις ενδιάμεσες ταχύτητες κίνησης ο κινητήρας δουλεύει αποδίδοντας μικρότερη της μέγιστης ισχύς, οπότε στο διάγραμμα θα ήταν σαν να είχαμε μικρότερο πλάτος τετραγώνου.
Καμπύλες ώσης
Για να δούμε λοιπόν στην πράξη πόση δύναμη φτάνει στο σημείο επαφής του ελαστικού με το δρόμο χρειαζόμαστε το διάγραμμα ώσης, για να το κατασκευάσουμε χρειαζόμαστε τα εξής:
- καμπύλη ισχύος
- λόγους μείωσης ταχυτήτων
- λόγο μείωσης ενδιάμεσου κιβωτίου*
- λόγο μείωσης διαφορικών
- διάμετρος τροχού
*transfer case, οι "αργες-γρήγορες" σχέσεις που έχουν πολλά τετρακίνητα μοντέλα
Με τα παραπάνω στοιχεία και με τη βοήθεια του τύπου που ακολουθεί προκύπτει το διάγραμμα ώσης,
ώση=(ισχύς/στροφές ανά λεπτό)*(λόγος μείωσης 1ης ταχύτητας)*(λόγος μείωσης transfer)*(λόγος μείωσης διαφορικού)*(2/διάμετρος τροχού) (ομοίως για 2α,3η κλπ)
Οι καμπύλες που προκύπτουν για κάθε ταχύτητα είναι:
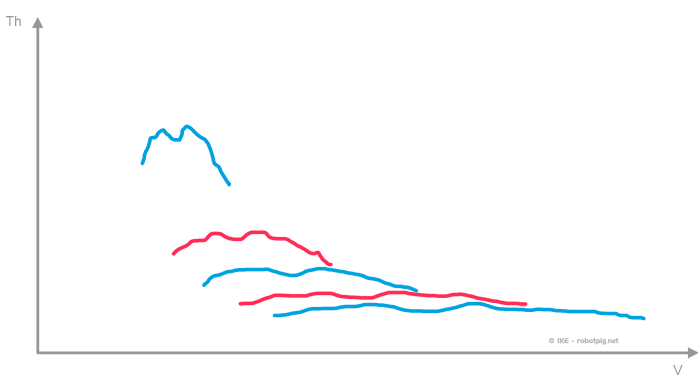
..και το ενιαίο σχήμα για όλες τις σχέσεις αντίστοιχα:
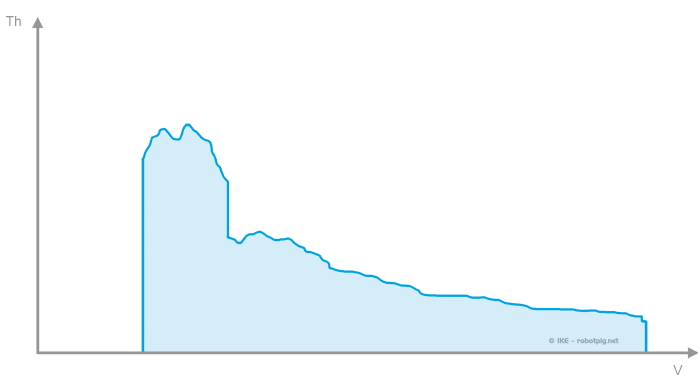
Το παραπάνω διάγραμμα έχει στον οριζόντιο άξονα την ταχύτητα κίνησης και στον κατακόρυφο την διαθέσιμη ώση (δύναμη) στους κινητήριους τροχούς.
Όπως είναι προφανές το διάγραμμα καμπύλων ώσης δεν είναι παρά το διάγραμμα της ισχύος ανηγμένο για κάθε σχέση του συστήματος μετάδοσης. Εδώ μπορούμε να εντοπίσουμε μια από τις συνηθέστερες παρεξηγήσεις:
Το να κρίνουμε πόσο δυνατό είναι ένα αυτοκίνητο με βάση την τιμή της μέγιστης ιπποδύναμης (ή ροπής) είναι σαν να πετάμε την καμπύλη από το διάγραμμα και να κρατάμε μόνο 5 (αν έχουμε 5τάχυτο κιβώτιο) σημεία. Και μάλιστα αν δεν συνυπολογίσουμε τα μεγέθη του συστήματος μετάδοσης δεν μπορούμε να έχουμε ούτε τα σημεία αυτά καθώς δεν θα γνωρίζουμε την θέση τους ούτε στον οριζόντιο ούτε στον κατακόρυφο άξονα. Αυτό που απομένει είναι ένα σημείο (αυτό της μέγιστης ισχύος) που στην πραγματικότητα από μόνο του δεν σημαίνει τίποτα.
Διαδρομή αναφοράς
Για να γίνουν τα παραπάνω πιο κατανοητά θα τα εφαρμόσουμε σε ένα παράδειγμα με αρκετές εφαρμογές ώστε να καλύψουμε τις περισσότερες περιπτώσεις. Για να δούμε λοιπόν πως μεταφράζεται το διάγραμμα ώσης στην πράξη θα το προβάλουμε σε μια διαδρομή αναφοράς.
Θεωρούμε την διαδρομή μιας μικρής πίστας, σχετικά κλειστής (για περισσότερα στο κουτάκι δίπλα) στην οποία ένας τυπικός γύρος μας δίνει το παρακάτω γράφημα με την ταχύτητα κίνησης του οχήματος σε κάθε σημείο:
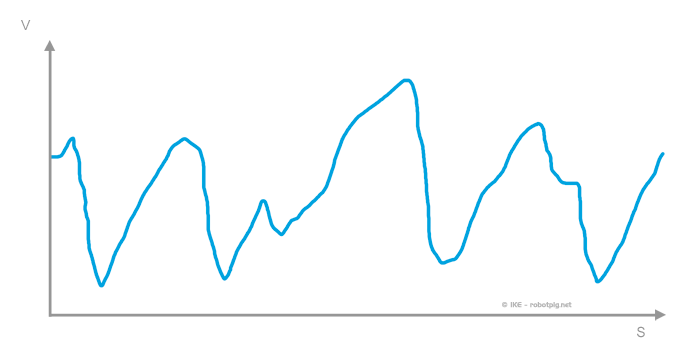
Αν αντιστοιχίσουμε την ώση για την ταχύτητα σε κάθε σημείο της πίστας (από το διάγραμμα ώσης πιο πάνω) θα έχουμε το διάγραμμα ώσης / απόστασης για τη συγκεκριμένη πίστα (και τις συγκεκριμένες ταχύτητες κίνησης!).
Έτσι μπορούμε να δούμε σε κάθε σημείο την 'περίσσεια ώσης' που έχει το όχημά μας. Όσο περισσότερη τόσο μεγαλύτερη η ικανότητα του αυτοκινήτου να επιταχύνει ή να έλκει φορτίο.
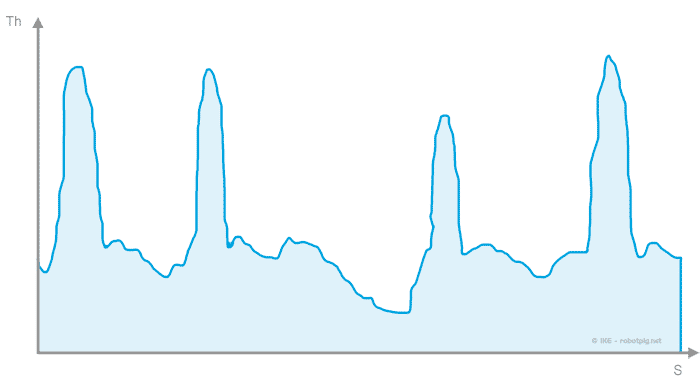
(Συνεχιζεται..)